在大三学习《机器学习》这门课程的时候，笔者对于L1、L2正则化并没有过多的深入讲解，只知道L0、L1产生稀疏的解，L2会产生稠密的解。以至于我在复习阶段一直以为是一特有的东西呢~~还不是不认真看书，明明书上讲了~~

最近在学习《深度学习》这门课程，由于课程之间融会贯通，再次碰到了这俩兄弟，于是我在查阅了相关资料之后，终于有所了解了，于是做了个笔记到这里。

范数

在了解L1、L2正则化之前，我们需要了解一下什么是范数。其实这里的L1、L2指的是L1范数、L2范数。范数(norm)是数学的一种基本概念，在泛函分析中，它定义在赋范线性空间中，并满足一定的条件，即①非负性；②齐次性；③三角不等式。它常常被用来度量某个向量空间（或矩阵）中的每个向量的长度或大小。

什么你说没看懂？没看懂就对了，我们从向量的范数公式来理解一下：

‖X‖_p=(∑_{i=1}^n|x_i|^p )^{\frac{1}{p}} \tag{1.1}

公式(1.1)则是p范数的数学表达。还是看不懂？，我们取几个特例来看一下：

‖X‖_0=x_1^0+x_2^0+x_3^0+...+x_n^0 (x_i\neq0) \tag{1.2}

对于L0范数，当x_i\neq0的时候，‖X‖_0相当于统计了样本个数，而当出现x_i=0的时候，舍弃掉该项，就能通过比较L0范数来比较一个有效样本量的多少了。

让我们来看看L1范数的公式：

‖X‖_1=|x_1|+ |x_2|+|x_3|+...+|x_n|\tag{1.3}

这里的|x_1|指的是模长，其实就是曼哈顿距离。相当于向量的L1范数是高维空间到原点的曼哈顿距离，对于二维坐标而言，在一个以原点为中心，倾斜45°的正方形上的向量L1范数是相等的。

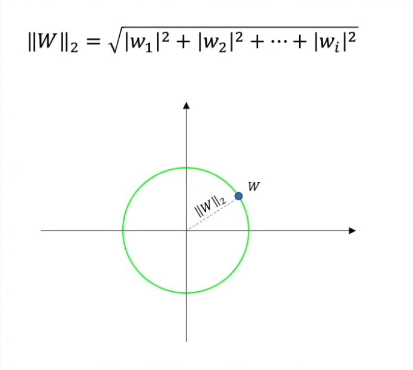
让我们来看看L2范数的公式：

‖X‖_2=\sqrt{x_1^2+x_2^2+x_3^2+...+x_n^2}\tag{1.4}

是不是感觉很熟悉？有点像是欧氏距离的定义？向量的L2范数是高维空间到原点的欧氏距离，对于二维坐标而言，距离原点同一距离的圆上的向量L2范数是相等的。

通过这几个例子来看，范数其实描述的是一种对向量大小或长度的一种度量！这么一说是不是就豁然开朗了呢？

有意思的是，∞范数的定义如下：

‖X‖_\infty=\max\{|x_1|,|x_2|,|x_3|,...|x_n|\}=\max_{1\le i\le m}{(|x_i|)} \tag{1.5}

意味着对向量的∞范数，该值为分量的最大值。

有关矩阵的范数，这里不做展开，可以参考该视频：向量范数与矩阵范数_哔哩哔哩_bilibili

正则化

知道L1、L2范数是什么之后，接下来我们来了解一下什么是正则化。

Regularization，中文翻译过来可以称为正则化，或者是规范化。我们都知道，对于一个模型的训练，我们需要构建其损失函数，通过在训练中使损失函数减小以得到模型能力的提升。而有时候损失函数太小会出现模型泛化能力太强，造成了过拟合的情况，此时我们有两种方法来实现缓解过拟合的方法：一是使用“早停”的方法，当训练集误差降低而验证集误差增高的时候停止模型的训练，以缓解过拟合的情况；二是使用“正则化”，在损失函数中加入约束条件，使其能够对过拟合有所缓解。

总而言之，言而总之，正则化是一种处理过拟合的方法，是在损失函数中通过添加特定项来约束损失函数，以防止过拟合的一种方法。

L1、L2正则化

说了这么多，对于一个训练好的模型，我们为什么还需要使用正则化？

这里我们借用王木头学科学的视频：“L1和L2正则化”直观理解(之一)，从拉格朗日乘数法角度进行理解_哔哩哔哩_bilibili

以神经网络训练为例，下图是简单的神经网络

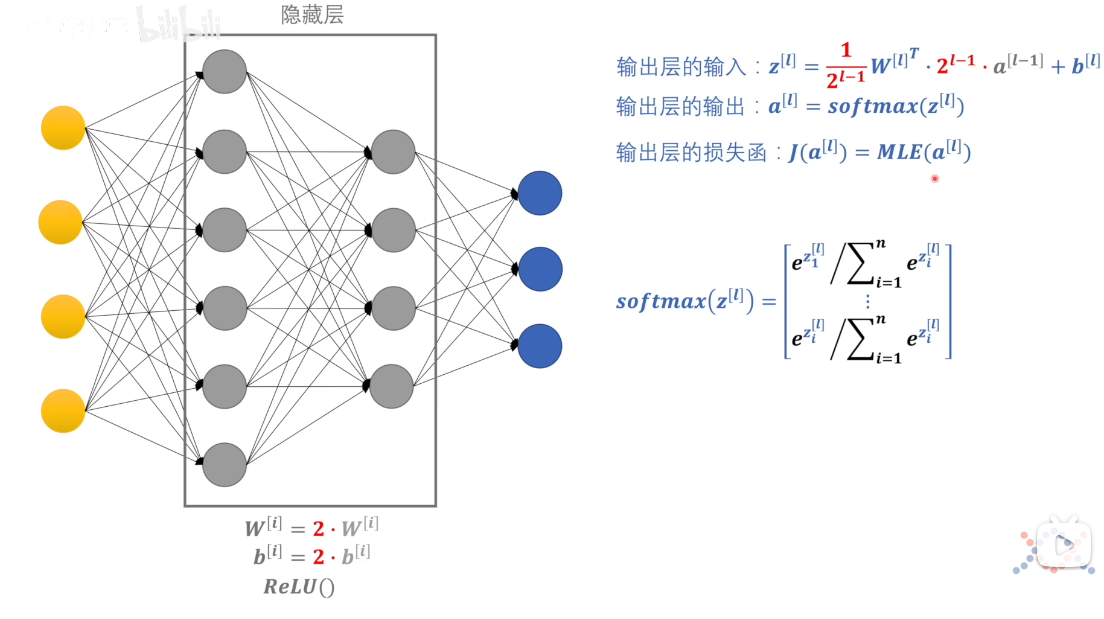
对该模型而言，对同一输入，最终损失函数的值是差不多的，而得到的权重和偏差w和b可能是不一样的，或大或小（如输出层的输入公式）。虽然损失函数值差不多，但是我们实际运用是基于测试集来验证模型的性能，而对于偏大或偏小的w和b的参数可能会导致在测试集上出现问题，例如当w和b参数为较大的参数，输入的数据的噪声和偏差也会同比例放大，从而降低模型的性能。

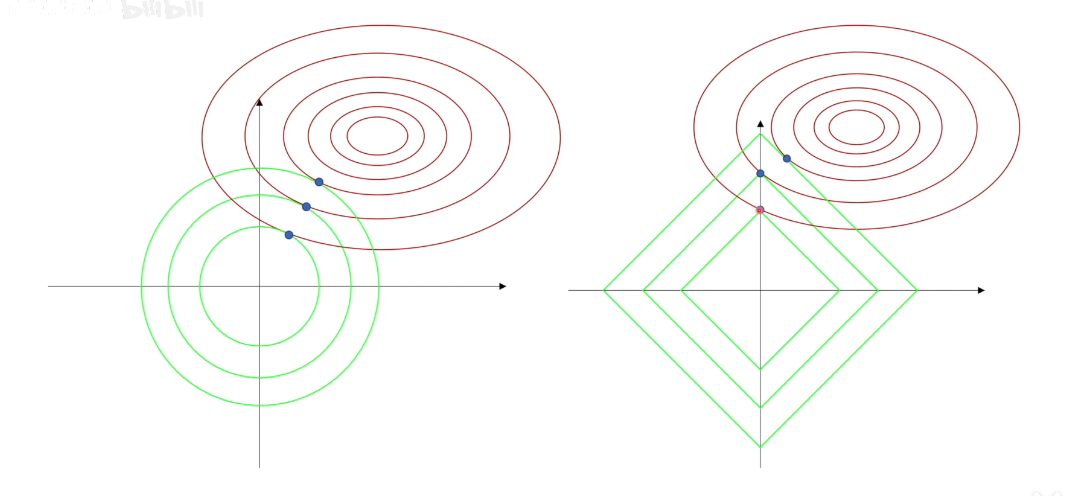
如何约束参数范围？我们可以人为的约束参数范围，如约束w的范围，在训练的过程中w与b相对应，约束w相当于约束b。如下图为L1、L2正则化的约束条件，红色的是损失函数等高线，绿色的框是可行域范围。当确定了可行域范围，我们就可以在约束条件下找到最值点。（以二维坐标轴为例）第一排为求解最值问题，我们使用拉格朗日乘数法转化为拉格朗日函数，使用拉格朗日函数来求解最值问题。

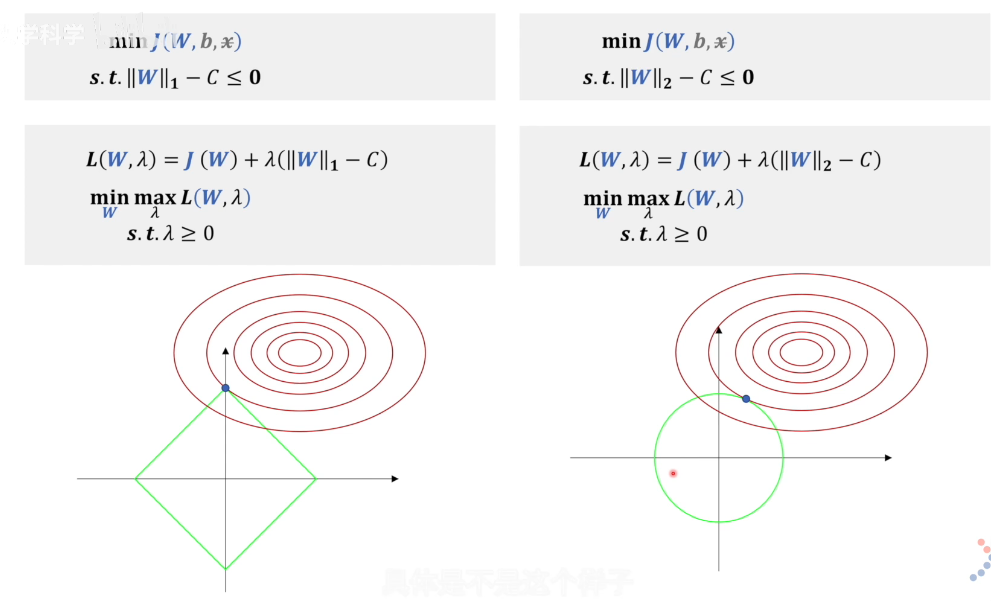
但是问题出现在这里：拉格朗日有两个未知的参数啊，我们怎么求解呢？我们构建红色的L，相对于绿色的L少了\lambda * C 常数项，这个是我们更多使用的L2正则化表达式。如何证明这两个拉格朗日函数的w最值的呢？我们通过对这两个函数求关于w的梯度，发现梯度是相等的，故我们求得的w参数是一样的。对于图像化理解，如右图所示，这里的\lambda‖X‖_2就是绿色的约束向量，J(w)就是红色的损失函数向量，通过调整\lambda的值来控制w的范围，从而实现约束参数的作用。