2.1 经验误差与过拟合

误差：学习器的实际预测输出与样本的真实输出之间的差异。在训练集上的误差称之为训练误差，在样本上的误差称之为泛化误差。

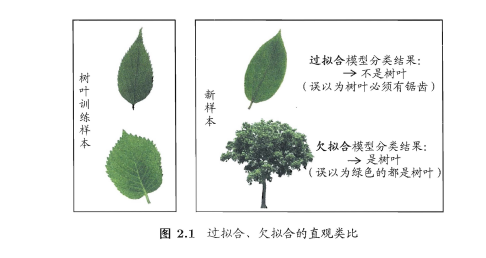
过拟合与欠拟合：用图说明。

2.2 评估方法

如何评估泛化误差：使用测试集来测试模型对新事物的学习能力。本节使用下列方法将测试集划分为训练集和测试集。

2.2.1 留出法

“留出法”直接将数据集D划分为两个互斥的集合，其中一个集合作为训练集S，另一个作为测试集T，即D=S\cup{T}， S\cap{T}=\emptyset。在S上训练出模型后，用T来评估其测试误差，作为对泛化误差的估计。其中，对于按比例划分数据集需要遵循分层采样的原理

2.2.2 交叉检验法

“交叉验证法”先将数据集D划分为k个大小相似的互斥子集，即D=D_1\cup{D_2}\cup{D_3}\cup...\cup{D_i} ，D_i\cup{D_j}=\emptyset . 每个子集D_i都尽可能保持数据分布的一致性，即从D中通过分层采样得到. 然后，每次用k-1个子集的并集作为训练集，余下的那个子集作为测试集。这样就可获得k组训练/测试集，从而可进行k次训练和测试，最终返回的是这k个测试结果的均值。不难发现对于交叉检验结果的稳定性很大程度上取决于k的取值，因此也称之为“k折交叉验证”。

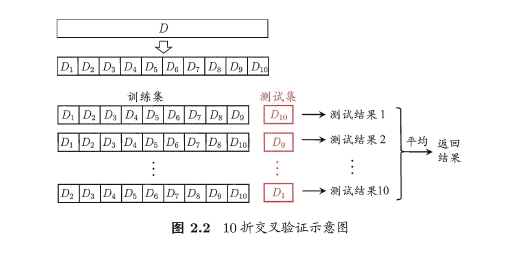
其中当子集个数k与样本个数m相等时，称之为留一法。

2.2.3 自助法

对于给定m样本的的数据集D，每次从中抽取一个样本，将其复制一份放入新数据集D‘中，重复操作m次来构建新的数据集。（类似于抽取并放回）对于对m样本被抽取到的概率为：

\lim_{m \to \infty}({1-\frac{1}{m}})^m\rightarrow\frac{1}{e}\approx0.368

2.3 性能度量

对学习器的泛化性能进行评估需要性能度量。在预测任务中，给定样例集D = {(X1, Y1) , (X2 ，Y2)， . . . , (Xm, Ym)} ，其中饥是示例Xi 的真实标记。要评估学习器f的性能，就要把学习器预测结果f(x)与真实标记y进行比较。回归任务最常用的性能度量是"均方误差"。

E(f:D)=\frac{1}{m}\sum^m_{i=1}{(f(x_i)-y_i)^2}

2.3.1 错误率与精度

错误率：E(f;D)=\frac{1}{m}\sum^m_{i=1}{Ⅱ(f(x_i)\ne{y_i})}

精度：acc(f;D)=\frac{1}{m}\sum^m_{i=1}{Ⅱ(f(x_i)={y_i})}=1-E(f;D)

2.3.2 查准率、查全率与F1

真实情况	预测结果
正例	反例
正例	TP（真正例）	FN（假正例）
反例	FP（假反例）	TN（真反例）

真实情况

预测结果

正例

反例

正例

TP（真正例）

FN（假正例）

反例

FP（假反例）

TN（真反例）

上表表示了在实际模型运行中分类结果的混淆矩阵。其中T代表True，F代表Fales，P代表Positive，N代表Negative。对应查准率Precision和查全率Recall分别如下。

P=\frac{TP}{TP+FP}

R=\frac{TP}{TP+FN}

查准率表示的是对于真实情况的正例中对应有多少比例为正例，而查全率则是对预测结果的正例中对应有多少比例的正例。二者相互矛盾，一般来说一者偏高另一者就会偏低。通过对以查准率为纵轴、查全率为横轴作图就得到了查准率-查全率曲线，简称"P-R 曲线"，显示该曲线的图称为"P-R图"。

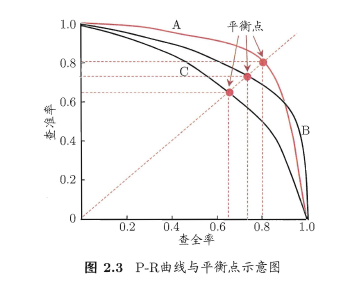
通过比较P-R曲线下的面积可以比较两个模型之间的性能。如图，模型A曲线完全包裹模型C，则可以认为模型A性能大于模型C。同时也可以选取查准率=查全率点来比较模型性能，该点对应查全率数值为“平衡点”。

对于更加精确的指标，F1度量如下：

F1=\frac{2\times{P}\times{R}}{P+R}

\frac{1}{F1}=\frac 1 2 (\frac 1 P+\frac 1 R)

而如果对于查准率或查全率有不同的偏好，可以使用F_{\beta}度量：

F_\beta=\frac{(1+\beta^2)\times{P}\times{R}}{(\beta^2\times P)+R}

\frac 1 {F_\beta}=\frac 1 {1+\beta^2}(\frac 1 P + \frac {\beta^2} R)

其本质是一种加权平均值。通过调整\beta的取值来控制度量对查全率和查准率的偏好。

2.3.3 ROC和AUC

模型对测试样本进行分类的时候，需要将预测值与阈值比较，大于阈值分为正类，反之则为反类。通过调整阈值，我们可以控制模型对样本预测的输出。而在不同任务中，我们需要根据不同需求来调整阈值。如果我们更重视"查准率"，则可选择排序中靠前的位置进行截断，对应更高阈值；若更重视"查全率"，则可选择靠后的位置进行截断，对应更低阈值。我们通过手动调节阈值，并计算真正例率TRP和假正例率FPR绘制出ROC曲线，定义分别为：

TPR=\frac {TP} {TP+FN}

FPR=\frac {FP} {TP+FP}

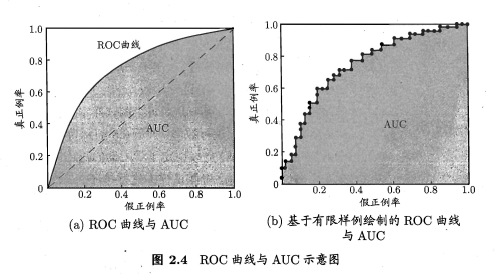
如上为ROC曲线，曲线下方阴影面积为AUC。与PR曲线类似，当一个模型的ROC曲线能够完全“包住”另一个模型，则说明前者性能大于后者性能。

2.3.4 代价敏感错误率

真实情况	预测类别
第0类	第1类
第0类	0	cost_{01}
第1类	cost_{10}	0

真实情况

预测类别

第0类

第1类

第0类

cost_{01}

第1类

cost_{10}

上表表示了当模型预测错误类别所需要的二分类代价矩阵。通过对系数的赋值来实现对分类任务调度代价敏感性能度量。代价敏感错误率公式则是在原有公式的基础上对不同错误分类乘以对应系数，在此不做赘述。

2.4 比较检验

该章节主要阐述了使用假设检验方法来比较两个模型性能的比较方法，主要偏向于数学，在此不做赘述。~~看不懂又懒得敲Latex导致的~~

2.5 偏差与方差

偏差方差分解是解释学习算法泛化性能的一种重要工具。

模型的泛化误差E(f;D)=bias^2(x)+var(x)+\varepsilon^2，其中bias(x)为偏差，var(x)为方差，\varepsilon为噪声。偏差-方差分解说明，泛化性能是由学习算法的能力、数据的充分性以及学习任务本身的难度所共同决定的。给定学习任务为了取得好的泛化性能，则需使偏差较小，即能够充分拟合数据，并且使方差较小，即使得数据扰动产生的影响小。

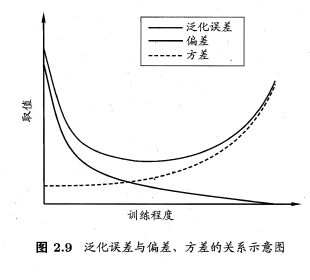
一般来说，偏差与方差是有冲突的，这称为偏差-方差窘境。给定学习任务，假定我们能控制学习算法的训练程度，则在训练不足时学习器的拟合能力不够强，训练数据的扰动不足以便学习器产生显著变化，此时偏差主导了泛化错误率；随着训练程度的加深，学习器的拟合能力逐渐增强，训练数据发生的扰动渐渐能被学习器学到，方差逐渐主导了泛化错误率；在训练程度充足后，学习器的拟合能力已非常强，训练数据发生的轻微扰动都会导致学习器发生显著变化，若训练数据自身的、非全局的特性被学习器学到了，则将发生过拟合。